Theory and Numerics of ODEs

3.2 First order linear autonomous equation

\(\text{ }\)\(\)Terminology In this section we will completely solve the class of first order linear autonomous ODEs. These are ODEs of the form \[\alpha\dot{y}(t)+\beta y(t)+\gamma=0,\tag{3.8}\] where \(\alpha,\beta,\gamma\in\mathbb{R},\alpha\ne0\) (\(\dot{y}\) is Newton’s notation, recall Section 2.4). Note that:

  1. The equation ([eq:ch3_fo_lin_aut-1]) is equivalent to \(G(\dot{y}(t),y(t))=0\) where \({G(y_{1},y_{0})=\alpha y_{1}+\beta y_{0}+\gamma}.\) This \(G\) is a linear function of \(y_{0},y_{1},\) hence linear equation.

  2. The highest order derivative that appears is the first derivative \(\dot{y}(t),\) hence first order (recall Definition 2.4).
  3. The function \(G(y_{1},y_{0})\) from 1. does not depend on \(t,\) hence autonomous (recall Definition 2.6).

The numbers \(\alpha,\beta,\gamma\) can be called coefficients. In the next section we will consider equations of the form ([eq:ch3_fo_lin_aut-1]) but where at least one of \(\alpha,\beta,\gamma\) is a non-trivial function \(\alpha(t),\beta(t),\gamma(t)\) of the independent variable \(t,\) rather than constants. These equations are no longer autonomous. Therefore an alternative terminology for the equation in ([eq:ch3_fo_lin_aut-1]) is “first order linear ODE with constant coefficients”. In later chapter we will study higher order linear equations, which take the form \({\sum_{i=0}^{k}\alpha_{i}(t)y^{(i)}(t)+\gamma(t)=0}.\)

Recall the ODE \[v'(t)=g-\frac{\gamma}{m}v(t),t\ge0,\tag{3.9}\] from Sections 1.1-1.3, which modelled an object falling subject to gravity and air resistance. This ODE is of the form ([eq:ch3_fo_lin_aut-1]) after the substitutions \[\alpha\to1,\quad\beta\to\frac{\gamma}{m},\quad\gamma\to-g.\]

One can always standardize ([eq:ch3_fo_lin_aut-1]) by dividing through by \(\alpha\) (as we are assuming \(\alpha\ne0\)) to arrive at the equation \(\dot{y}(t)+\frac{\beta}{\alpha}y(t)+\frac{\gamma}{\alpha}=0.\) It’s convenient to further rearrange this to \(\dot{y}(t)=-\frac{\beta}{\alpha}y(t)-\frac{\gamma}{\alpha}.\) We arrive at the following formal definition.

Definition 3.10 • First order linear autonomous ODE

We call any equation of the form \[\dot{y}(t)=ay(t)+b,\quad\quad t\in I,\tag{3.10}\] for \(a,b\in\mathbb{R}\) and any interval \(I\subset\mathbb{R}\) a first order linear autonomous ODE.

\(\text{ }\)Interpretation Recall that the derivative \(\dot{y}(t)\) of a function can be interpreted as the instantaneous rate of change of the function. In a very small time interval \([t,t+\varepsilon)\) the function changes roughly by \(\varepsilon\dot{y}(t).\) One can interpret the terms on the r.h.s of ([eq:fo_lin_aut_def_eq]) as follows:

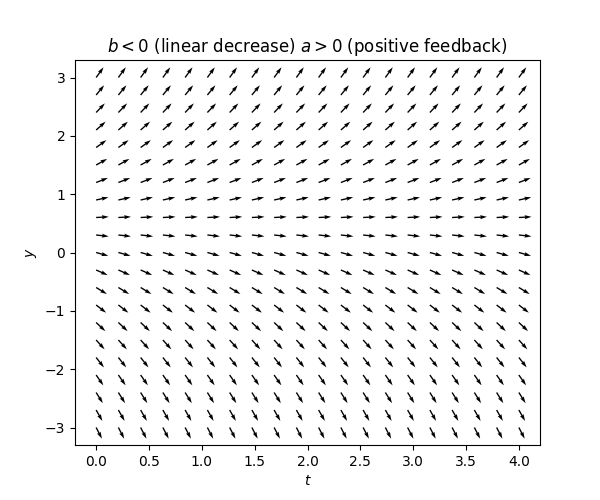
  1. The term \(b\) represents an instantaneous absolute rate of change. Instantaneous simply because the derivative is the instantaneous rate of change of \(y(t).\) Absolute in the sense that whatever the value of \(y(t)\) is, this rate stays the same. If \(b>0\) it’s an absolute rate of increase and if \(b<0\) it’s an absolute rate of decrease.

  2. The term \(ay(t)\) is a feedback.

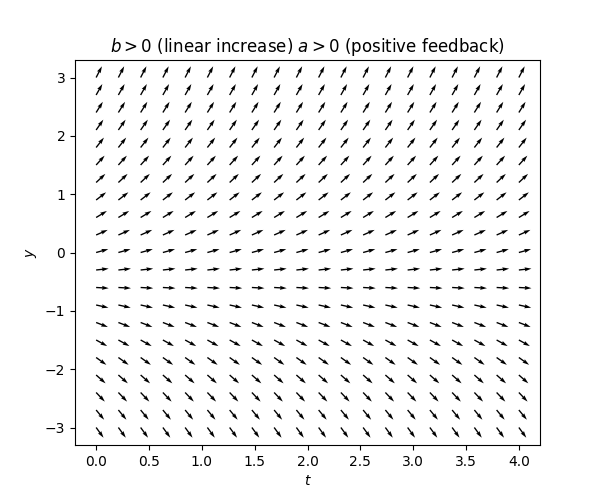
    1. If \(a>0\) a positive feedback: the term \(ay(t)\) has the same sign as \(y(t),\) so it “tries to” make \(\dot{y}(t)\) also have this sign and thus “pushes” \(y(t)\) in the direction of increased magnitude,

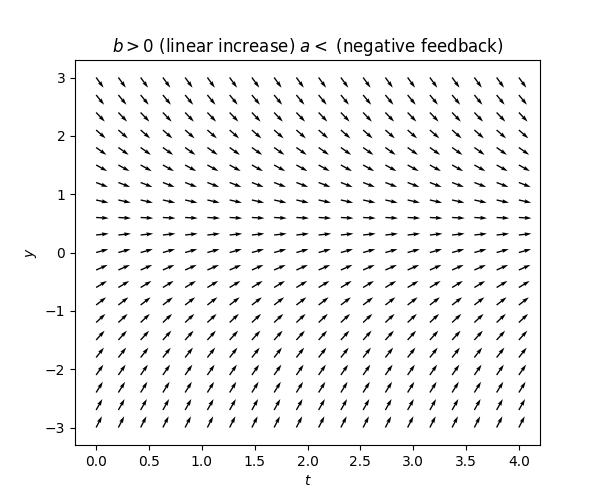
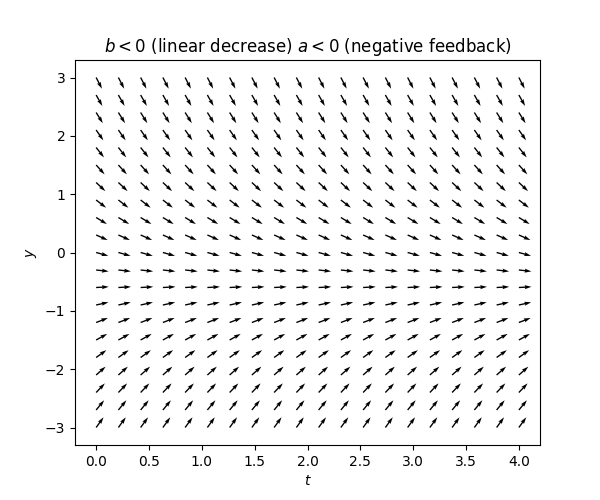
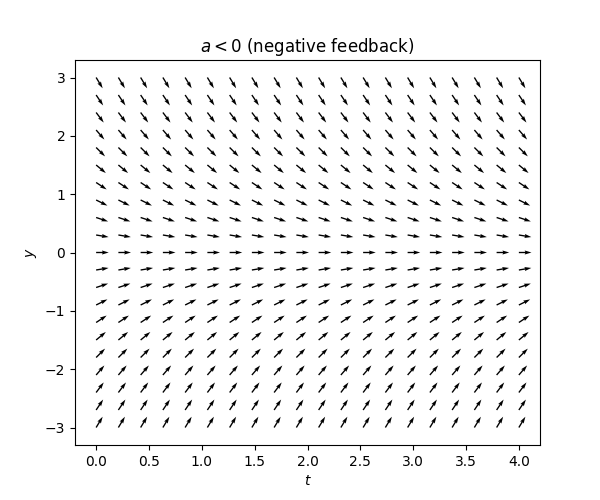
    2. If \(a<0\) a negative feedback: the term \(ay(t)\) has the opposite sign of \(y(t),\) so it “tries to” make \(\dot{y}(t)\) also have the opposite sign and thus “pushes \(y(t)\)” in the direction of decreased magnitude.

  3. An even more precise description of the term \(ay(t)\) is that it represents a instantaneous relative rate of range (as opposed to the absolute rate of change embodied by the term \(b\)). Relative because the amount of change is effectively given by a percentage of the current value of \(y(t),\) or in other words a proportion (namely the proportion \(a\)) of the current value of \(y(t).\)

One can see this reflected in the tangent fields of such equations:

Figure 3.30: Tangent field of first order linear autonomous equation \(\dot{y}(t)=ay(t)+b\) in different scenarios for \(a,b.\)
Example 3.11 • Population dynamics - positive feedback

We model the concentration of a bacterium reproducing in the blood of a patient under the following assumptions:

  1. for each bacterium on average four child bacteria are produced per hour,

  2. each hour one bacterium per mL of blood enters the blood stream from outside4.

We refrain from modelling the effect of the immune system, or a more realistic non-constant rate of infection. Under these assumptions we let \(p(t)\) denote the concentration of bacteria per mL when \(t\) hours have passed since the patient first came into contact with the bacterium. The rate of growth of this concentration at time \(t\) is \(\dot{p}(t).\) We decompose this rate as \(\theta_{r}+\theta_{i},\) where \(\theta_{r}\) corresponds to growth due to reproduction, i.e. (1) above, and \(\theta_{i}\) corresponds to growth due to particles entering the blood from outside (“immigration” of bacteria), i.e. (2) above.

  1. The assumption (1) can be interpreted as \(\theta_{r}=3p(t),\) since the net increase of bacteria per hour due to one bacterium is \(\text{\#child bacteria}-1=4-1=3\) .

  2. The assumption (2) can be interpreted as \(\theta_{i}=1.\)

Thus we have arrived at the ODE model: \[\dot{p}(t)=3p(t)+1.\tag{3.11}\] The expression ([eq:ch3_bacteria]) is a first order autonomous ODE, as defined in Definition 3.10, with \(a=3\) and \(b=1\)). The “feedback” corresponding to (1), (1’), \(3p(t)\) is positive - more bacteria means faster rate growth. Indeed \(a>0.\)
Example 3.12 • Gravity and air resistance - negative feedback The model ([eq:ch3_ode_grav_air_res-1]) of the velocity of an object subject to gravity and air resistance is an example where there is a negative feedback: for higher velocity air resistance increases. Indeed if written in the form of Definition 3.10 it has \(a=-\frac{\gamma}{m}<0.\)
\(\text{ }\)Seeking solutions. In Section 1.3 we saw that ([eq:ch3_ode_grav_air_res-1]) has a stationary solution. It’s immediate to check that every first order linear autonomous ODE was in ([eq:fo_lin_aut_def_eq]) has a stationary solution: make the ansatz \(y(t)=u\) for arbitrary \(u\in\mathbb{R},\) so that \(\dot{y}(t)=0,\) and then plug into ([eq:fo_lin_aut_def_eq]) to arrive at \[0=ua+b,\] which is equivalent to \(u=-\frac{b}{a}.\) Thus5 \[y(t)=-\frac{b}{a},\tag{3.12}\] is a solution to ([eq:fo_lin_aut_def_eq]) (for \(a\ne0\) - the simpler special case case \(a=0\) is addressed at the end of the section).

It is instructive to study solutions \(y(t)\) of ([eq:fo_lin_aut_def_eq]) via the “recentered” solutions \[x(t)=y(t)-\left(-\frac{b}{a}\right)\quad\quad t\in I,\tag{3.13}\] which represent the deviation of \(y(t)\) from the stationary solution at time \(t.\) If \(y(t)\) is a solution then \(x(t)\) satisfies \(\dot{x}(t)=\dot{y}(t)=ay(t)+b=a(y(t)+\frac{b}{a})=ax(t),\) i.e. \(x(t)\) is a solution to \[\dot{x}(t)=ax(t).\tag{3.14}\] Furthermore if \(x(t)\) is a solution to ([eq:fo_lin_aut_recentered]) then \(y(t)=x(t)+\frac{b}{a}\) is a solution of ([eq:fo_lin_aut_def_eq]) (verify this!). The equation ([eq:fo_lin_aut_recentered]) is ([eq:fo_lin_aut_def_eq]) with \(b=0,\) so we have reduced the general case with \(a\ne0,b\in\mathbb{R}\) to the case \(a\ne0,b=0.\) Note that ([eq:fo_lin_aut_recentered]) has the stationary solution \(x(t)=0,\) which makes sense since our change of variables ([eq:fo_lin_aut_cov]) has shifted all solutions down by \(-\frac{b}{a}.\)

If \(x(t)\) is a solution to ([eq:fo_lin_aut_recentered]) then \(\alpha x(t)\) is also a solution for any \(\alpha\in\mathbb{R}.\) This is not the case for the original ([eq:fo_lin_aut_def_eq]). When we study higher order linear ODEs this property will play an important role - linear ODEs that have it will be called “homogeneous”.

The tangent field for the equation ([eq:fo_lin_aut_recentered]) is simply the tangent fields from Figure Figure 3.11 shifted:

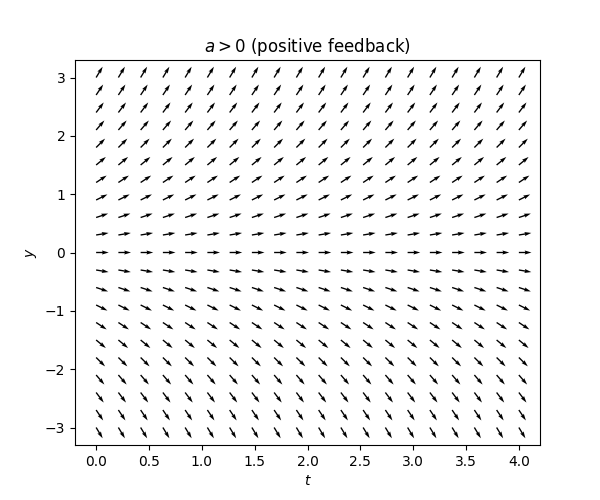
Figure 3.31: Tangent field of the first order linear autonomous equation \(\dot{x}(t)=ax(t)\) in different scenarios for \(a.\)

\(\text{ }\)Solution for positive feedback - \(a>0.\) From the tangent field labeled \(a>0\) in Figure Figure 3.12 we may guess that the curves traced out by the tangent is of the form \(e^{ct}\) for a positive \(c>0.\) Making the ansatz \(x(t)=e^{ct}\) and plugging into ([eq:fo_lin_aut_recentered]) we obtain that \(\dot{x}(t)=ce^{ct}=ax(t)\) for all \(t\in I\) iff \(a=c,\) and thus determine that \(x(t)=e^{at}\) is a solution. Using the property mentioned above, also \[x(t)=\alpha e^{at}\tag{3.15}\] is a solution for any \(\alpha\in\mathbb{R}.\) Going back to ([eq:ch3_fo_lin_aut-1]) this implies that \[y(t)=\alpha e^{at}-\frac{b}{a}\tag{3.16}\] is a solution for any \(\alpha\in\mathbb{R}.\) These solutions can be interpreted as functions diverging exponentially at rate \(e^{at}\) away from the stationary solution \(-\frac{b}{a}.\)

Solution for negative feedback -

\(a<0.\) In this case it is instructive to highlight the negativity of the coefficient \(a\) by writing ([eq:fo_lin_aut_recentered]) in the equivalent form \[\dot{x}(t)=-|a|x(t).\tag{3.17}\]

From the tangent field labeled \(a<0\) in Figure Figure 3.12 we may guess that ([eq:ch3_fo_lin_aut_recent_a_neg]) has solutions of the form \[x(t)=e^{-ct}\text{\,for a }c>0.\tag{3.18}\] We in fact already did precisely this for ([eq:ch3_ode_grav_air_res-1]) in Section 1.3. Making the ansatz \(x(t)=e^{-ct}\) and plugging into ([eq:fo_lin_aut_recentered]) we obtain that \(\dot{x}(t)=-ce^{-ct}=-|a|x(t)\) for all \(t\in I\) iff \(|a|=c,\) and thus determine that \(x(t)=e^{-|a|t}\) is a solution. Therefore also \[x(t)=\alpha e^{-|a|t}\tag{3.19}\] is a solution for any \(\alpha\in\mathbb{R},\) and \[y(t)=\alpha e^{-|a|t}-\frac{b}{a}\tag{3.20}\] is a solution to ([eq:ch3_fo_lin_aut-1]). These solutions can be interpreted as functions converging exponentially at rate \(e^{-at}\) to the stationary solution \(-\frac{b}{a}.\)

In retrospect we see that we in fact made the same ansatz whether \(a>0,a<0,\) just with a different sign in the argument for the exponential. Whatever the sign of \(a\) we could thus simply have made the ansatz \(x(t)=e^{ct}\) for \(c\in\mathbb{R}\) and arrived at \[x(t)=\alpha e^{at},\tag{3.21}\] as a solution to ([eq:fo_lin_aut_recentered]) and \[y(t)=\alpha e^{at}-\frac{b}{a},\tag{3.22}\] as a solution to ([eq:fo_lin_aut_def_eq]) for any \(a\ne0.\)

\(\text{ }\)Ruling out other solutions. We have found the infinite family of solutions ([eq:ch3_fo_lin_aut_form_of_sol]) to ([eq:fo_lin_aut_def_eq]). Are there any other solutions? In fact, there are not! The functions ([eq:ch3_fo_lin_aut_form_of_sol]) form an exhaustive set of solutions. For the first order autonomous equations studies in this section this can be proven by an elementary argument.

Proposition 3.13

(Complete solution of first order autonomous ODEs with \(a\ne0\)). Assume \(a,b\in\mathbb{R},a\ne0\) and \(I\subset\mathbb{R}\) an interval. Then a function \(y(t)\) is a solution of the ODE \[\dot{y}(t)=ay(t)+b,\quad\quad t\in I,\tag{3.23}\] iff \[y(t)=\alpha e^{at}-\frac{b}{a}\quad\forall t\in I,\text{ for some }\alpha\in\mathbb{R}.\tag{3.24}\]

Proof. \(\impliedby\) : If \(y(t)\) has the form ([eq:ch3_fo_lin_aut_uniquness_sol_form]) then \(\dot{y}(t)=a\alpha e^{at}\) and \(ay(t)+b=a(\alpha e^{at}-\frac{b}{a})+b=a\alpha e^{at}-b+b=a\alpha e^{at}=\dot{y}(t),\) so indeed \(y(t)\) solves the ODE ([eq:ch3_fo_lin_aut_uniquness_ODE_form]) .

\(\implies\): Let \(y(t)\) be any solution of ([eq:ch3_fo_lin_aut_uniquness_ODE_form]). Consider \[z(t)=e^{-at}\left(y(t)+\frac{b}{a}\right).\tag{3.25}\] Using the product rule to differentiate \(z(t)\) we obtain \[\dot{z}(t)=-ae^{-at}\left(y(t)+\frac{b}{a}\right)+e^{-at}\dot{y}(t)\text{\,for all }t\in I.\] Using that \(y(t)\) is a solution of ([eq:ch3_fo_lin_aut_uniquness_ODE_form]) by replacing \(\dot{y}(t)\) is the previous equation by the r.h.s. of ([eq:ch3_fo_lin_aut_uniquness_ODE_form]) this implies that \[\dot{z}(t)=-ae^{-at}\left(y(t)+\frac{b}{a}\right)+e^{-at}\left(ay(t)+b\right)=0\text{ for all }t\in I.\] Any differentiable function on an interval \(I\) with vanishing derivative is constant (by the fundamental theorem of calculus). Thus there is a constant \(\alpha\) such that \(z(t)=\alpha\) for all \(t\in I,\) and so \[e^{at}\left(y(t)+\frac{b}{a}\right)=\alpha\text{ for all }t\in I.\tag{3.26}\] Rearranging this implies that \(y(t)\) satisfies ([eq:ch3_fo_lin_aut_uniquness_sol_form]).

\(\text{ }\)Initial Value Problems. Typically when modelling with ODEs one imposes additional constraints beyond the differential equation itself. For instance for the ODE of Example in Section 1.1 we imposed the constraint \[v(0)=0\] on the ODE ([eq:ch3_ode_grav_air_res-1]), signifying that we assume the object is at rest at time \(t=0.\) Similarly for Example 3.11 the constraint \[p(0)=0\] is natural, signifying that there are no bacteria present in the blood stream at \(t=0.\) In the general stetting of Definition 3.10 one can consider constraints of the form \[y(t_{0})=y_{0},\tag{3.27}\] where \(t_{0}\) is the left-end point of the interval \(I\) (which is \([0,\infty)\) for both Example 3.11 and Example 3.12). We make the following formal definition.
Definition 3.14 • First order linear autonomous IVP

We call any equation of the form \[\dot{y}(t)=ay(t)+b\quad\quad t\in I,\tag{3.28}\] for \(a,b\in\mathbb{R}\) and any interval \(I\subset\mathbb{R}\) subject to the constraint \[y(t_{0})=y_{0},\tag{3.29}\] where \(t_{0}\) is the left-endpoint of \(I\) and \(y_{0}\in\mathbb{R},\) a first order linear autonomous Initial Value Problem (IVP).

If a solution of the form ([eq:ch3_fo_lin_aut_uniquness_sol_form]) is to satisfy ([eq:fo_lin_aut_IVP_def_IVP_cond]), it must hold that \[\alpha e^{at_{0}}-\frac{b}{a}=y_{0}.\] This equation can be solved for \(\alpha\) to obtain \[\alpha=e^{-at_{0}}\left(y_{0}+\frac{b}{a}\right).\] With this value for \(\alpha\) the solution \(y(t)\) becomes \[y(t)=e^{a(t-t_{0})}\left(y_{0}+\frac{b}{a}\right)-\frac{b}{a}.\tag{3.30}\] The function ([eq:ch3_fo_aut_IVP_sol]) is a solution to the ODE ([eq:fo_lin_aut_def_eq]) subject to the constraint ([eq:ch3_fo_lin_aut_IVP_cond]). It follows by the previous lemma, and the fact that \(\alpha\) above is unique, that this is the unique solution.

Proposition 3.15 • Unique solution of first order linear autonomous ODEs with constraint

Assume \(a,b\in\mathbb{R},\) \(a\ne0,\) \(I\subset\mathbb{R}\) an interval \(t_{*}\in I\) and \(y_{0}\in\mathbb{R}.\) Then the ODE \[\dot{y}(t)=ay(t)+b\quad t\in I,\tag{3.31}\] subject to the constraint \[y(t_{*})=y_{0},\tag{3.32}\] has the unique solution \[y(t)=\left(y_{0}+\frac{b}{a}\right)e^{a(t-t_{*})}-\frac{b}{a}\quad\forall t\in I.\tag{3.33}\]

Proof. \(\impliedby\) Proposition 3.13 with \(\alpha=y_{0}+\frac{b}{a}\) implies that if \(y(t)\) is as in ([eq:ch3_fo_lin_aut_IVP_uniq_sol]) then it is a solution to ([eq:ch3_fo_lin_aut_IVP_uniq_ODE_cond]). Furthermore if \(y(t)\) is given by ([eq:ch3_fo_lin_aut_IVP_uniq_sol]) then \[y(t_{*})=\left(y_{0}+\frac{b}{a}\right)e^{a(t_{*}-t_{*})}-\frac{b}{a}=y_{0}+\frac{b}{a}-\frac{b}{a}=y_{0},\] so the constraint ([eq:ch3_fo_lin_aut_IVP_uniq_IVP_cond]) is satisfied. \(\implies\) By Proposition 3.13, any solution to ([eq:ch3_fo_lin_aut_IVP_uniq_ODE_cond]) has the form ([eq:ch3_fo_lin_aut_uniquness_sol_form]) for some \(\alpha.\) If \(y(t)\) also satisfies the constraint ([eq:ch3_fo_lin_aut_IVP_uniq_IVP_cond]) then it must hold that \[\alpha e^{at_{*}}-\frac{b}{a}=y_{0},\] which implies \(\alpha=e^{-at_{*}}\left(y_{0}+\frac{b}{a}\right)\) and thus that \(y(t)\) satisfies ([eq:ch3_fo_lin_aut_IVP_uniq_sol]).

Remark 3.16

a) In exercise \(1.\) on exercise sheet \(2\) you will practice solving this kind of ODE.
b) If you are solving a given concrete first order linear autonomous ODE, it is recommended that you make the ansatz \(y(t)=Ae^{Bt}+C\) and then solve for \(A,B,C\) that satisfy the ODE and any constraints you may want to satisfy, rather than memorizing and using the explicit formula ([eq:ch3_fo_lin_aut_IVP_uniq_sol]). The implicit general form \(y(t)=Ae^{Bt}+C\) is easier to remember, the computation using it will be less error prone, and if you ever need the general explicit formula ([eq:ch3_fo_lin_aut_IVP_uniq_sol]) you easily rederive it from the former implicit form.

In the present setting we obtain this strong existence and uniqueness result thanks to the elementary argument of Proposition 3.13. Later, for more general ODEs, we will not be so lucky. A general first order IVP has the form \[\dot{y}(t)=H(t,y(t)),\quad\quad t\in I,\quad\text{subject to the constraint }y(t_{0})=y_{0}.\tag{3.34}\] In a later chapter we will determine conditions on \(H\) for a solution to exist and be unique, but in the most general setting we can obtain such guarantees only locally - for times in a possibly small neighborhood of \(t_{0},\) rather than in the whole interval \(I\) as in the previous lemma. Note that we can even take \(I=\mathbb{R}\) in all the above results.

\(\text{ }\)No feedback - special case \(a=0\) The above results dealt with the main case of the ODE ([eq:fo_lin_aut_def_eq]), which is \(a\ne0.\) For completeness we finish by handling the case \(a=0,\) for which the solutions behave differently - they are linear functions.

Lemma 3.17

(Solution of first order autonomous ODEs with \(a=0\)). Assume \(b\in\mathbb{R}\) and \(I\subset\mathbb{R}\) an interval. Then a function \(y\) is a solution of the ODE \[\dot{y}(t)+b=0,\quad\quad t\in I,\] iff \[y(t)=\alpha-bt\quad\forall t\in I,\text{ for some }\alpha\in\mathbb{R}.\]

Proof. Exercise (exercise 2 on exercise sheet 2).

3.3 Explicit and implicit ODEs

Definition 2.4 defines an ODE in the form \[G(t,y^{(k)}(t),y^{(k-1)}(t),\ldots,y^{'}(t),y(t))=0,\quad\quad t\in I,\tag{3.35}\] for an arbitrary function \(G:\mathbb{R}^{k+2}\to\mathbb{R}.\) An ODE written in this form is called an implicit ODE. An ODE written in the alternative form \[y^{(k)}=H(t,y^{(k-1)}(t),\ldots,y^{(0)}(t))=0,\quad\quad t\in I,\tag{3.36}\] for6 \(H:\mathbb{R}^{k+1}\to\mathbb{R}\) is called an explicit ODE. The ODE ([eq:ch3_implicit_eq]) constrains the value of \(y^{(k)}(t)\) via an implicit relation (akin to defining a circle in the plane implicitly by the relation \(x^{2}+y^{2}=1\)), while the ODE ([eq:ch3_explicit_eq]) specifies the value of \(y^{(k)}(t)\) as an explicit function of the other variables \(t,y^{(k-1)}(t),\ldots,y^{(0)}(t)\) (akin to defining a circle in the plane explicitly as \(\left\{ (\sin(\theta),\cos(\theta)):0\le\theta\le2\pi\right\}\)).

The implicit form ([eq:ch3_implicit_eq]) is more general: every explicit ODE of the form ([eq:ch3_explicit_eq]) is also of the form ([eq:ch3_implicit_eq]) with \(G(t,y_{k},\ldots,y_{0})=y_{k}-H(t,y_{k-1},\ldots,y_{0}).\) Sometimes an ODE written in the implicit form ([eq:ch3_implicit_eq]) can conversely easily be written in the explicit form ([eq:ch3_explicit_eq]). This was the case in the previous section where the ODEs \[\alpha\dot{y}(t)+\beta y(t)+\gamma=0,\quad\quad t\in I,\] (see ([eq:ch3_fo_lin_aut-1]); this is an implicit relation) with constant coefficients and \(\alpha\ne0\) were seen to be equivalent to an ODE of the form \[\dot{y}(t)=ay+b,\quad\quad t\in I,\] (see ([eq:fo_lin_aut_def_eq]); this is explicit). Another such example is the implicit ODE \[(1+t^{2})\ddot{y}(t)+\dot{y}(t)y(t)=5,\quad\quad t\in\mathbb{R},\tag{3.37}\] corresponding to ([eq:ch3_implicit_eq]) with \(k=2\) and \(G(t,y_{2},y_{1},y_{0})=(1+t)^{2}y_{2}+y_{1}y_{0}-5.\) Since the coefficient \(1+t^{2}\)of \(\ddot{y}(t)\) is everywhere positive the relation ([eq:ch3_non_lin_implicit_ex]) can be solved for \(\ddot{y}(t)\) to obtain \[\ddot{y}(t)+\frac{\dot{y}(t)y(t)-5}{1+t^{2}}=0,\quad\quad t\in\mathbb{R},\] which is of the explicit form ([eq:ch3_explicit_eq]) with \(H(t,y_{1},y_{0})=-\frac{y_{1}y_{0}-5}{1+t^{2}}.\)

But for instance the ODE written implicitly as \[t\ddot{y}(t)+\dot{y}(t)y(t)=5,\quad\quad t\in[-1,1],\] can not be directly written explicitly on the interval \([-1,1],\) since we can not divide through by the coefficient \(t\) for \(t=0.\) Another such example is the implicitly written ODE \[(\dot{y}(t))^{2}-y(t)^{2}-1=0,\quad\quad t\in[0,\infty).\tag{3.38}\] The condition ([eq:ch3_non_lim_implicit_ex_not_explicit]) is equivalent to \[\dot{y}(t)=\pm\sqrt{1+y(t)^{2}},\quad\quad t\in[0,\infty),\] which is not of the form ([eq:ch3_explicit_eq]) for a single function \(H,\) because of the \(\pm\) coming from the two possible square roots.

A first order explicit ODE is simply the case \(k=1\) of ([eq:ch3_explicit_eq]).

Definition 3.18 • First order explicit ODE and IVP

We call any ODE of the form \[\dot{x}(t)=H(t,x(t)),\quad\quad t\in I,\tag{3.40}\] for a function \(H:\mathbb{R}^{2}\to\mathbb{R}\) and interval \(I\subset\mathbb{R}\) an explicit first order ODE.

We call any ODE of the form \[\dot{x}(t)=H(x(t)),\quad\quad t\in I,\tag{3.41}\] for a function \(H:\mathbb{R}\to\mathbb{R}\) and interval \(I\subset\mathbb{R}\) an explicit first order autonomous ODE.

We call ([eq:def_ch3_fo_explicit]) or ([eq:def_ch3_fo_aut]) together with the constraint \[x(t_{0})=x_{0},\tag{3.42}\] where \(t_{0}\) is the left-endpoint of \(I\) and \(x_{0}\in\mathbb{R}\) an explicit first order Initial Value Problem (IVP).

Compare ([eq:def_ch3_fo_explicit]) to ([eqn:ODE_def]), ([eq:def_ch3_fo_aut]) to ([eq:ODE_def-1]) and ([eq:def_ch3_fo_explicit_IVP]) to ([eq:fo_lin_aut_IVP_def_IVP_cond]). This form of ODE has already been mentioned in passing in ([eq:ch3_tf_first_order_aut_explicit]) and ([eq:ch3_preview_fo_general_IVP]). In the next few sections we will study explicit first order ODEs like ([eq:def_ch3_fo_explicit]). Before the end of the chapter will consider the implicit first order linear equations \(\alpha(t)\dot{y}(t)+\beta(t)y(t)+\gamma(t)=0.\)

3.4 Interlude - Leibniz rule for differentiating under the integral sign

When solving non-autonomous first order linear equations in the next section we will need to compute derivatives of the form \[\frac{d}{dt}\int_{s}^{t}f(r,t)dr.\] The classical formula for these is known as Leibniz rule. Recall that the fundamental theorem of calculus addresses the case when \(f\) does not depend on \(t,\) and states that \[\frac{d}{dt}\int_{s}^{t}f(r)dr=f(t)\tag{3.43}\] for any Lebesgue integrable function \(f.\) Leibniz rule is the following.

Theorem 3.19 • Leibniz rule

If \(I\subset\mathbb{R}\) is an open interval and \(f:I^{2}\to\mathbb{R}\) is such that \(f(r,t)\) is continuous in \(I^{2},\) and the partial derivative \(\partial_{t}f(r,t)\) exists and is continuous in \(I^{2},\) then the derivative \(\frac{d}{dt}\int_{s}^{t}f(r,t)dr\) is well-defined for all \(s,t\in I,s\le t,\) and \[\frac{d}{dt}\int_{s}^{t}f(r,t)dr=f(t,t)+\int_{s}^{t}\partial_{t}f(r,t)dr.\]

Remark 3.20

Heuristically this formula may be derived by using the Taylor expansion \[f(r,t+\varepsilon)=f(r,t)+\varepsilon\partial_{t}f(r,t)+O(\varepsilon^{2}),\] and using the definition of the derivative as the limit \[\lim_{\varepsilon\to0}\varepsilon^{-1}\left(\int_{s}^{t+\varepsilon}f(r,t+\varepsilon)dr-\int_{s}^{t}f(r,t)dr\right),\] together with the fundamental theorem of calculus ([eq:ftoc]).

3.5 Explicit first order linear non-autonomous equations

\(\text{ }\)Terminology In this section we solve explicit first order linear ODEs essentially completely, including non-autonomous equations. These are the ODEs that satisfy the following definition, which extends Definition 3.10 by allowing the coefficients \(a,b\) to be functions of the independent variable \(t,\) and is a special case of Definition 3.18.
Definition 3.21 • Explicit first order linear ODE

We call any equation of the form \[\dot{y}(t)=a(t)y(t)+b(t),\quad\quad t\in I,\tag{3.45}\] for any interval \(I\subset\mathbb{R}\) and functions \(a,b:I\to\mathbb{R}\) an explicit first order linear ODE.

We actually find explicit formulas for the solutions, which are somewhat related to those of Section 3.2 for the autonomous case, albeit somewhat more complex.

An implicit first order linear ODE has the aforementioned form \[\alpha(t)\dot{y}(t)+\beta y(t)+\gamma(t)=0,\quad\quad t\in I,\tag{3.46}\] for functions \(\alpha,\beta,\gamma:I\to\mathbb{R}.\) If \(\alpha(t)\ne0\) for all \(t\in I\) this ODE can equivalently be written in the explicit form of Definition 3.21 with \(a(t)=-\frac{\beta(t)}{\alpha(t)},b(t)=-\frac{\gamma(t)}{\alpha(t)}.\) If \(\alpha(\hat{t})=0\) for some \(\hat{t}\in I\) this can’t be done, and solutions to the implicit ODE ([eq:implicit_fo_lin]) will exhibit different behavior than an explicit ODE like ([eq:fo_lin_def_eq]) close to \(\hat{t}.\) In a later section of this chapter we will study such implicit ODEs.

\(\text{ }\)Interpretation. One can interpret the ODE ([eq:fo_lin_def_eq]) as follows.

\(\text{ }\)Solution when \(b(t)=0\) We consider first the case \(b(t)=0\) of ([eq:fo_lin_def_eq]), namely \[\dot{x}(t)=a(t)x(t),\quad\quad t\in I.\tag{3.47}\] This is ([eq:fo_lin_aut_recentered]) with a non-constant coefficient \(a(t).\) As for ([eq:fo_lin_aut_recentered]), if \(x(t)\) is a solution to ([eq:ch3_fo_lin_b_zero]) then so is \(t\to\alpha x(t)\) for any \(\alpha\in\mathbb{R}.\)

\(\text{ }\)Heuristic derivation of ansatz. Assume for simplicity that \(I=[0,1]\) and assume that \(a(t)\) is constant on the two intervals \([0,\frac{1}{2})\) and \([\frac{1}{2},1]\) taking values \(a_{1}\) and \(a_{2}\) respectively, i.e. \[a(t)=\begin{cases} a_{1} & \text{ if }t\in[0,\frac{1}{2}),\\ a_{2} & \text{ if }t\in[\frac{1}{2},1]. \end{cases}\tag{3.48}\] The expression ([eq:ch3_fo_lin_b_zero]) then implies that on the first interval \(x_{1}(t)=x(t)\) satisfies the ODE \[\dot{x}_{1}(t)=a_{1}x_{1}(t),\quad\quad t\in[0,\frac{1}{2}],\tag{3.49}\] and on the second interval \(x_{2}(t)=x(t)\) satisfies the ODE \[\dot{x}_{2}(t)=a_{2}x_{2}(t),\quad\quad t\in[\frac{1}{2},1].\tag{3.50}\] These are both first order linear autonomous ODEs. If we add the constraint \(x_{1}(0)=x_{0}\) for some \(x_{0}\in\mathbb{R}\) to ([eq:ch3_fo_lin_interval1]) it comes an IVP. The natural continuity constraint \(x_{2}(\frac{1}{2})=x_{1}(\frac{1}{2})\) turns ([eq:ch3_fo_lin_interval2]) into an IVP. Using Proposition 3.15 we obtain that the unique solution to the first IVP corresponding to ([eq:ch3_fo_lin_interval1]) is \[x_{1}(t)=e^{ta_{1}}x_{0},\quad\quad t\in[0,\frac{1}{2}),\] and the unique solution to the second IVP corresponding to ([eq:ch3_fo_lin_interval2]) is \[x_{2}(t)=e^{(t-\frac{1}{2})a_{2}}x_{1}(\frac{1}{2}),\quad\quad t\in[\frac{1}{2},1).\] Combining these we obtain \[x(t)=\begin{cases} e^{ta_{1}}x_{0} & \text{ if }t\in[0,\frac{1}{2}],\\ e^{(t-\frac{1}{2})a_{2}+\frac{1}{2}a_{1}}x_{0} & \text{ if }t\in[\frac{1}{2},1]. \end{cases}\tag{3.51}\] This formula makes a lot of sense in terms of the interpretation of \(a(t)\) as an instantaneous relative rate of change: for \(t\in[0,\frac{1}{2}]\) this instantaneous rate is \(a_{1}\) and the cumulative instantaneous relative change after time \(t\) is \(t\times a_{1}.\) After \(t=\frac{1}{2}\) the instantaneous relative rate of change shifts to \(a_{2},\) and the cumulative instantaneous relative change is that from the interval \([0,\frac{1}{2}],\) which amounts to \(\frac{1}{2}a_{1},\) plus that of the second interval which is \((t-\frac{1}{2})\times a_{2}.\) Note furthermore that for the piece-wise constant \(a\) as in ([eq:ch3_a_t_peicewise_constant]) \[\begin{array}{lcl} ta_{1} & = & \int_{0}^{t}a(s)ds\text{\,for }t\in[0,\frac{1}{2}],\\ (t-\frac{1}{2})a_{2}+\frac{1}{2}a_{1} & = & \int_{0}^{t}a(s)ds\text{\,for }t\in[\frac{1}{2},1], \end{array}\] so that ([eq:ch3_a_t_peicewise_constant]) can be expressed as \[x(t)=e^{\int_{0}^{t}a(s)ds}x(0).\tag{3.52}\] Also this formula makes a lot of sense heuristically:

The second point makes sense for any (integrable) \(a(t),\) piece-wise constant or not. Thus it makes sense to try ([eq:ch3_fo_lin_b_zero_ansatz_interval_0_1]) as an ansatz for a solution of ([eq:ch3_fo_lin_b_zero]) for general \(a(t).\)

\(\text{ }\)Trying ansatz for \(b(t)=0.\) For a general interval \(I\) and any \(t_{0}\in I\) consider \[x(t)=e^{\int_{t_{0}}^{t}a(r)dr}x(t_{0}),\tag{3.53}\] the natural generalization of the ansatz ([eq:ch3_fo_lin_b_zero_ansatz_interval_0_1]). Using the chain rule and the fundamental theorem of calculus we have that if \(x(t)\) is as in ([eq:ch3_fo_lin_b_zero_ansatz]) then \[\dot{x}(t)=\left(\frac{d}{dt}\int_{t_{0}}^{t}a(r)dr\right)e^{\int_{t_{0}}^{t}a(r)dr}x_{0}=a(t)e^{\int_{t_{0}}^{t}a(r)dr}x_{0}=a(t)x(t).\] Thus this \(x(t)\) is indeed a solution to ([eq:ch3_fo_lin_b_zero])! (Rigorous details such as whether \(\frac{d}{dt}\int_{t_{0}}^{t}a(r)dr\) is well-defined will be dealt in the proof of the formal statement of this result - Proposition 3.24 below).

\(\text{ }\)Heuristically deriving ansatz for \(b(t)\ne0\) Recall that we interpret \(b(t)\) as an instantaneous absolute rate of change. Over a small time interval \([t,t+\varepsilon)\) the cumulative absolute change can be thought of as approximately \(\varepsilon b(t).\) Heuristically, things become simpler if we imagine instead that the whole absolute change of magnitude \(\sim\varepsilon b(t)\) happens in one instantaneous jump at the start of the time interval, at time \(t.\) For instance, we can imagine jumps of size \(\varepsilon b(t_{n})\) at times \(t_{0}+n\varepsilon.\) In this case a solution between the jump times, in the open interval \((t_{n},t_{n+1})\) would evolve as ([eq:ch3_fo_lin_b_zero]), without a \(b(t)\) term. Then at time \(t=t_{n+1}\) one would have a sudden increase from \(y(t_{n+1}^{-})\) (the left limit as \(t=t_{n+1})\) to \(y(t_{n+1}^{+})=y(t_{n+1}^{-})+\varepsilon b(t_{n+1})\) (the right limit at \(t=t_{n+1}\)), and then in the time interval \((t_{n+1},t_{n+2})\) the solution would evolve as ([eq:ch3_fo_lin_b_zero]) again.

Let \(x_{1}(t),x_{2}(t)\) be two solutions to ([eq:ch3_fo_lin_b_zero]) with \(x_{1}(t_{n+1})=x_{1,0}\) and \(x_{2}(t_{n+1})=x_{2,0}.\) Consider \(x(t)=x_{1}(t)+x_{2}(t).\) Then \[\dot{x}(t)=\dot{x}_{1}(t)+\dot{x}_{2}(t)=a(t)x_{1}(t)+a(t)x_{2}(t)=a(t)\left(x_{1}(t)+x_{2}(t)\right)=a(t)x(t),\] so \(x\) is also a solution to ([eq:ch3_fo_lin_b_zero]) but with \(x(t_{n+1})=x_{1}(t_{n+1})+x_{2}(t_{n+1})=x_{1,0}+x_{2,0}.\) This is another way in which ([eq:ch3_fo_lin_b_zero]) is a linear equation: for \(b(t)=0\) linear combinations of solutions are new solutions - more on this the upcoming chapter on higher order linear ODEs. Returning to the evolution in the time intervals \((t_{n},t_{n+1})\) and \((t_{n+1},t_{n+2})\) if one assumes a sudden increase from \(y(t_{n+1}^{-})\) to \(y(t_{n+1}^{-})+\varepsilon b(t_{n+1})\) at time \(t=t_{n+1},\) one has with \(x_{1,0}=y(t_{n+1}^{-})\) and \(x_{2,0}=\varepsilon b(t_{n+1})\) that \(x(t)=x_{1}(t)+x_{2}(t)\) solves to ([eq:ch3_fo_lin_b_zero]) on the interval7 \([t_{n+1},t_{n+2}]\) with the IVP condition \(x(t_{n+1})=y(t_{n+1}^{-})+\varepsilon b(t_{n+1}),\) the value after the jump. A solution in the interval \((t_{n+1},t_{n+2})\) of this “jumping ODE” would thus be \[y(t)=y(t_{n+1}^{-})e^{\int_{t_{n+1}}^{t}a(s)ds}+\varepsilon b(t_{n+1})e^{\int_{t_{n+1}}^{t}a(s)ds},\quad\quad t\in(t_{n+1},t_{n+2}).\tag{3.54}\] Considering similarly the interval \((t_{n},t_{n+1})\) \[y(t_{n+1}^{-})=e^{\int_{t_{n}}^{t_{n+1}}a(s)ds}y(t_{n}^{-})+\varepsilon b(t_{n})e^{\int_{t_{n}}^{t_{n+1}}a(s)ds},\] and plugging this into ([eq:ch3_fo_lin_heuristic_b_non_zero_interval_t_n+1_t_n+2]) would give \[y(t)=y(t_{n}^{-})e^{\int_{t_{n}}^{t}a(s)ds}+\varepsilon b(t_{n})e^{\int_{t_{n}}^{t}a(s)ds}+\varepsilon b(t_{n+1})e^{\int_{t_{n+1}}^{t}a(s)ds},\quad\quad t\in(t_{n+1},t_{n+2}).\]

Continuing in the same manner for \(n-1,n-2,\ldots,0\) and multiplying out would give \[y(t)=y(t_{0}^{-})e^{\int_{t_{0}}^{t}a(s)ds}+\varepsilon\sum_{k=0}^{n}b(t_{k})e^{\int_{t_{k}}^{t}a(s)ds},\quad\quad t\in(t_{n+1},t_{n+2}).\]

Here the interpretation is that at time \(t_{k}\) the level of \(y(t)\) jumps by \(\varepsilon b(t_{k}),\) and the size of the jump then evolves as the ODE \(\dot{x}(t)=a(t)x(t)\) until the time \(t,\) giving a final contribution of \(\varepsilon b(t_{k})e^{\int_{t_{k}}^{t}a(s)ds}.\) The sum in this expression can be thought of as a Riemann sum which approximates the integral \(\int_{0}^{t}b(r)e^{\int_{r}^{t}a(s)ds}dr,\) which is a well-defined quantity also in our original setting of function \(b(t)\) representing an instantaneous absolute rate of increase without any “jumping”. This leads us to the ansatz \[y(t)=y(t_{0})e^{\int_{t_{0}}^{t}a(s)ds}+\int_{t_{0}}^{t}b(r)e^{\int_{r}^{t}a(s)ds}dr,\quad\quad t\in I,\tag{3.55}\] with the interpret that at time \(r\) an “infinitesimal amount” \(b(r)\) is added to \(y(t),\) and this contribution then evolves in the interval \([r,t]\) as the ODE \(\dot{x}(t)=a(t)x(t).\)

As a preliminary sanity check we compute ([eq:ch3_fo_lin_b_non_zero_final_ansatz]) when \(a(t),b(t)\) are constant, i.e. for the autonomous case of Section 3.2. Then \[e^{\int_{t_{0}}^{t}a(s)ds}=e^{(t-t_{0})a},\] and \[\int_{t_{0}}^{t}b(r)e^{\int_{r}^{t}a(s)ds}dr=b\int_{t_{0}}^{t}e^{(t-r)a}dr=b\frac{-e^{(t-r)a}}{a}|_{t_{0}}^{t}=\frac{b}{a}(-1+e^{(t-t_{0})a}),\] so that the r.h.s of ([eq:ch3_fo_lin_b_non_zero_final_ansatz]) promisingly reduces to the already proved formula \[e^{(t-t_{0})a}y(t_{0})+\frac{b}{a}(-1+e^{(t-t_{0})a})=e^{(t-t_{0})a}\left(y(t_{0})+\frac{b}{a}\right)-\frac{b}{a},\] for the autonomous case cf. ([eq:ch3_fo_lin_aut_IVP_uniq_sol]) of Proposition 3.15. \(\text{ }\)Trying ansatz for \(b(t)\ne0.\) We now try the ansatz ([eq:ch3_fo_lin_b_non_zero_final_ansatz]). Assuming for now that these integrals are well-defined an differentiable (we will check this in detail in the proof Proposition 3.24 below), we note that by the chain rule and fundamental theorem of calculus \[\frac{d}{dt}e^{\int_{t_{0}}^{t}a(r)dr}y(t_{0})=a(t)e^{\int_{t_{0}}^{t}a(r)dr}y(t_{0}).\] This means that for the first term of the ansatz ([eq:ch3_fo_lin_b_non_zero_final_ansatz]) \[\frac{d}{dt}e^{\int_{t_{0}}^{t}a(r)dr}y(t_{0})=a(t)\left(y(t)-\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du\right).\] Next by Leibniz’s rule (Theorem 3.19) applied with \(f(u,t)=e^{\int_{u}^{t}a(r)dr}b(u)\) we obtain \[\frac{d}{dt}\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du=f(t,t)+\int_{t_{0}}^{t}\partial_{t}f(u,t)du.\] Now since \(\int_{t}^{t}a(r)dr=0\) and \(\partial_{t}f(u,t)=a(t)e^{\int_{u}^{t}a(r)dr}b(u)\) this implies for the second term of the ansatz ([eq:ch3_fo_lin_b_non_zero_final_ansatz]) \[\frac{d}{dt}\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du=b(t)+a(t)\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du.\] Thus for \(y\) as in ([eq:ch3_fo_lin_b_non_zero_final_ansatz]) \[\dot{y}(t)=a(t)\left(y(t)-\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du\right)+b(t)+a(t)\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du.\] Note that terms involving \(\int_{t_{0}}^{t}e^{\int_{u}^{t}a(r)dr}b(u)du\) on the r.h.s. “magically” cancel, so that indeed \[\dot{y}(t)=a(t)y(t)+b(t)!\] Thus the ansatz ([eq:ch3_fo_lin_b_non_zero_final_ansatz]) indeed gives a solution (modulo technicalities which we check in detail in Proposition 3.24 below). We have thus found a family of solutions of the ODE ([eq:fo_lin_def_eq]). Like for the autonomous case, it turns out that these are all the solutions! Furthermore this can be proved by a generalization of the proof of the equivalent result for the autonomous case, Proposition 3.13. We first prove some preparatory lemmas.

The fundamental theorem of calculus implies the following.

Lemma 3.22

If \(a:I\to\mathbb{R}\) is continuous and Lebesgue integrable then \(t\to e^{\int_{r}^{t}a(s)ds}\) is continuous and differentiable in \(I,\) and \[\frac{d}{dt}e^{\int_{r}^{t}a(s)ds}=a(t)e^{\int_{r}^{t}a(s)ds},\quad\quad t\in I.\]

Leibniz’s rule implies the following.

Lemma 3.23

Let \(I\subset\mathbb{R}\) be an interval and let \(a,b:I\to\mathbb{R}\) be continuous and Lebesgue integrable on \(I.\) Then \[t\to\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr,\quad\quad t\in I,\] is well-defined and differentiable, and \[\frac{d}{dt}\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr=b(t)+a(t)\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr.\tag{3.58}\]

Proof. Let \(f(r,t)=e^{\int_{r}^{t}a(s)ds}b(r)\) so that \[\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr=\int_{t_{0}}^{t}f(r,t)dr.\] By Lemma 3.22 and our assumption on \(a\) the functions \(t\to e^{\int_{r}^{t}a(s)ds}\) and \(t\to\frac{d}{dt}e^{\int_{r}^{t}a(s)ds}\) are well-defined and continuous in \(I.\) Thus \(\partial_{t}f(r,t)\) is well-defined for \(t\in I\) and \(\partial_{t}f(r,t)=a(t)e^{\int_{r}^{t}a(s)ds}b(r).\) Since also \(b\) is continuous we thus have that \(f(r,t)\) and \(\partial_{t}f(r,t)\) are continuous and bounded on \(I.\) We can therefore apply Leibniz rule (Theorem 3.19) for this \(f(r,t).\) Note that \[f(t,t)=e^{\int_{t}^{t}a(s)ds}b(t)=b(t),\] since \(\int_{t}^{t}a(s)ds=0,\) and \[\int_{t_{0}}^{t}\partial_{t}f(r,t)dr=a(t)\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr.\] Thus Leibniz rule implies ([eq:ch3_use_of_leibniz]).

We are now ready to prove to characterize all solutions to the first order linear ODE ([eq:fo_lin_def_eq]).

Proposition 3.24

Let \(I\subset\mathbb{R}\) be an interval and let \(a,b:I\to\mathbb{R}\) be continuous and Lebesgue integrable on \(I.\)

A function \(y:I\to\mathbb{R}\) is a solution to the ODE \[\dot{y}(t)=a(t)y(t)+b(t),\quad\quad t\in I,\tag{3.60}\] iff \[y(t)=\alpha e^{\int_{t_{0}}^{t}a(s)ds}+\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr,\quad\quad t\in I,\tag{3.61}\] for some \(\alpha\in\mathbb{R}.\)

Proof. \(\impliedby\) Assume that \(y\) satisfies ([eq:ch3_prop_fo_lin_all_sols_sol_formn]) for some \(\alpha\in\mathbb{R}.\) By the assumptions on \(a,b\) Lemma 3.22 and Lemma 3.23 imply that the derivative \(\dot{y}(t)\) exists and \[\begin{array}{ccl} \dot{y}(t) & = & \alpha a(t)e^{\int_{t_{0}}^{t}a(s)ds}+b(t)+a(t)\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\\ & = & a(t)\left(\alpha e^{\int_{t_{0}}^{t}a(s)ds}+\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right)+b(t)\\ & = & a(t)y(t)+b(t), \end{array}\] for all \(t\in I,\) proving that \(y(t)\) is a solution of ([eq:ch3_prop_fo_lin_all_sols_ODE_form]). \(\implies\): Let \(y(t)\) be any solution of ([eq:ch3_prop_fo_lin_all_sols_ODE_form]). Consider \[z(t)=e^{-\int_{t_{0}}^{t}a(s)ds}\left(y(t)-\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right).\tag{3.62}\] As above the assumptions on \(a,b\) imply that \(t\to e^{\int_{t_{0}}^{t}a(s)ds}\) and \(t\to\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\) are differentiable. Using the product rule we obtain \[\dot{z}(t)=\left(\frac{d}{dt}e^{-\int_{t_{0}}^{t}a(s)ds}\right)\left(y(t)-\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right)+e^{-\int_{t_{0}}^{t}a(s)ds}\left(\dot{y}(t)-\frac{d}{dt}\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right),\] for all \(t\in I.\) Using Lemma 3.22 and Lemma 3.23 the r.h.s. equals \[-a(t)e^{-\int_{t_{0}}^{t}a(s)ds}\left(y(t)-\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right)+e^{-\int_{t_{0}}^{t}a(s)ds}\left(\dot{y}(t)-b(t)-a(t)\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right),\] for all \(t\in I.\) Since \(y\) is a solution of ([eq:ch3_prop_fo_lin_all_sols_ODE_form]) this in turns equals \[-a(t)e^{-\int_{t_{0}}^{t}a(s)ds}\left(y(t)-\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right)+e^{-\int_{t_{0}}^{t}a(s)ds}\left(a(t)y(t)-a(t)\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr\right),\] for all \(t\in I.\) Note that all terms on the r.h.s. cancel! Thus \[\dot{z}(t)=0\text{ for all }t\in I,\tag{3.63}\] which implies that \(z(t)=\alpha\) for some \(\alpha,\) and thus that \(y(t)\) has the form ([eq:ch3_prop_fo_lin_all_sols_sol_formn]).

Also similarly to the autonomous case, we get uniqueness of the solution to IVPs.

Corollary 3.25

Let \(I\subset\mathbb{R}\) be an interval and let \(a,b:I\to\mathbb{R}\) be continuous and Lebesgue integrable on \(I.\) A function \(y:I\to\mathbb{R}\) is a solution to the IVP \[\dot{y}(t)=a(t)y(t)+b(t),\quad\quad t\in I,\quad\quad y(t_{0})=y_{0},\] iff \[y(t)=y_{0}e^{\int_{t_{0}}^{t}a(s)ds}+\int_{t_{0}}^{t}e^{\int_{r}^{t}a(s)ds}b(r)dr,\quad\quad t\in I.\]

Proof. Exercise: Adapt the proof of Proposition 3.15.
This is a very strong result: it proves existence of solutions globally on the whole interval \(I,\) and also uniqueness on this interval. As already mentioned after the corresponding result Proposition 3.15 for the autonomous case, for general first order ODEs we can only hope for a existence an uniqueness result that is local in character and thus significantly weaker.

Some of the problems in exercise 3, 4, 5 on exercise sheet 2 can be solved with the methods of this section.

3.6 Separable first order equations

Separable first order equations are an important class of ODE that admit quite explicit solutions even beyond linear case of the last section. In this context it is convenient to use Leibniz’s notation \(\frac{dy}{dx}\) for the derivative.

\(\text{ }\)Trivially separable ODE. Consider the ODE \[\frac{dy}{dx}=x^{3},\quad\quad x\in\mathbb{R},\tag{3.65}\] for an unknown function \(y.\) This is a trivial ODE, because the r.h.s. does not depend on \(y,\) only on the independent variable \(x.\) It is thus a simple integration problem: integrating both sides against \(x\) we obtain using the fundamental theorem of calculus for the l.h.s. that \[\int_{a}^{b}\frac{dy}{dx}dx=y(b)-y(a),\text{\,for all }a,b\in\mathbb{R},\tag{3.66}\] and for the r.h.s. that \[\int_{a}^{b}x^{3}dx=\frac{x^{4}}{4}|_{a}^{b}=\frac{b^{4}}{4}-\frac{a^{4}}{4},\text{\,for all }a,b\in\mathbb{R}.\tag{3.67}\] Thus any solution to ([eq:ch3_sep_trivial_example]) must satisfy \[y(b)-y(a)=\frac{b^{4}}{4}-\frac{a^{4}}{4}\text{\,for all }a,b\in\mathbb{R}.\] This implies that \[y(x)=c+\frac{x^{4}}{4},\tag{3.68}\] for the constant \(c=y(a)-\frac{a^{4}}{4}.\) It is easy to check that for any \(c\in\mathbb{R},\) the function ([eq:ch3_fo_sep_just_integration]) indeed satisfies ([eq:ch3_sep_trivial_example]). One could more quickly arrive at ([eq:ch3_fo_sep_just_integration]) by using the indefinite integrals \(\int\frac{dy}{dx}dx=y(x)+c'\) and \(\int xdx=\frac{x^{2}}{2}+c'',\) where arbitrary constants appear because indefinite integrals are only defined up to additive constant.

\(\text{ }\) Non-trivial separable ODE. Consider now the ODE \[\frac{dy}{dx}=6y^{2}x,\quad\quad x\in\mathbb{R}.\tag{3.69}\] Here is a very powerful heuristic trick to guess solutions of such an equation. Pretend that \(\frac{dy}{dx}\) is a fraction of two “infinitesimal variables” \(dx\) and \(dy,\) which it properly speaking is not: it is the derivative of \(y\) with respect to \(x,\) and \(dx\) and \(dy\) have no proper meaning if they appear by themselves, outside an integral like in ([eq:ch3_sep_trivial_rhs]) and ([eq:ch3_sep_trivial_lhs]) (in the integral the notation simply indicates which variable is integrated over, it does not represent a variable itself). Nevertheless, “squinting” and treating \(dy\) and \(dx\) as if they were variables we can multiply both sides of the equation by \(dx\) and cancel \(dx\) on the l.h.s. to obtain \["dy=6y^{2}xdx".\tag{3.70}\] The quotation marks indicate that this not a proper mathematically well-defined equation, only a heuristic way to rewrite the ([eq:ch3_sep_first_example]) . We can then divide through by \(y^{2},\) to obtain \["\frac{dy}{y^{2}}=6xdx".\tag{3.71}\] Now let us apply an indefinite integral to both sides \["\int\frac{dy}{y^{2}}=6\int xdx+c".\tag{3.72}\] The constant \(c\) appears since an indefinite integral is only defined up to additive constant.This is a well-defined expression: both sides are integrals with proper rigorous mathematical meaning! But the quotation marks remain because of the non-rigorous heuristic derivation that led to ([eq:ch3_sep_first_example_res]). We can compute both integrals in ([eq:ch3_sep_first_example_res]): \[\int\frac{dy}{y^{2}}=-\frac{1}{y}\text{ and }\int xdx=\frac{x^{2}}{2}.\tag{3.73}\] Combing these with ([eq:ch3_sep_first_example_res]) gives \["-\frac{1}{y}=3x^{2}+c".\tag{3.74}\] Solving for \(y\) gives \["y=\frac{1}{c-3x^{2}}".\tag{3.75}\]

\(\text{ }\) Trying ansatz. We can now consider this expression an ansatz for a solution of ([eq:ch3_sep_first_example]), i.e. we assume that \[y(x)=\frac{1}{c-3x^{2}},\tag{3.76}\] for some \(c\in\mathbb{R}.\) For this \(y(x)\) we have \[6y^{2}x=6\left(\frac{1}{c-3x^{2}}\right)^{2}x=\frac{6x}{(c-3x^{2})^{2}}.\] Furthermore using the chain rule we obtain \[\frac{dy}{dx}=-\frac{\frac{d}{dx}\left(c-3x^{2}\right)}{\left(c-3x^{2}\right)^{2}}=\frac{6x}{(c-3x^{2})^{2}}-.\] Thus indeed this \(y(x)\) satisfies the ODE ([eq:ch3_sep_first_example])! At least, on any interval \(I\) where \(y(x)\) as in ([eq:ch3_fo_sep_first_example_ansatz]) is well-defined and differentiable. This interval depends on \(c.\) If \(c<0\) then ([eq:ch3_fo_sep_first_example_ansatz]) is well-defined on the whole real line so one can take \(I=\mathbb{R}.\) If \(c\ge0\) then ([eq:ch3_fo_sep_first_example_ansatz]) is well-defined except when \(c=3x^{2},\) i.e. for \(x=\pm\sqrt{\frac{c}{3}}.\) Thus ([eq:ch3_fo_sep_first_example_ansatz]) is well-defined and differentiable on the three intervals \((-\infty,-\sqrt{\frac{c}{3}}),(-\sqrt{\frac{c}{3}},\sqrt{\frac{c}{3}})\) and \((\sqrt{\frac{c}{3}},\infty),\) and solves the ODE ([eq:ch3_sep_first_example]) on these intervals.

\(\text{ }\) Separable IVP. We can also use this family of solutions to derive solutions to IVPs such as \[\frac{dy}{dx}=6y^{2}x,\quad\quad y(0)=1.\tag{3.77}\] We seek a \(c\) such that \[\frac{1}{c-3x^{2}}=1\] when \(x=0,\) which simply means that \(c=1.\) Thus \[y(x)=\frac{1}{1-3x^{2}},\tag{3.78}\] is a solution to the IVP ([eq:ch3_fo_first_example_IVP]). However, we must once again be careful about the interval where the solution is defined and satisfies the ODE: in this case it is \([0,\frac{1}{\sqrt{3}}).\) As \(t\uparrow\frac{1}{\sqrt{3}}\) the solution ([eq:ch3_fo_first_example_IVP_sol]) diverges to \(\infty,\) and therefore is not defined for \(t=\frac{1}{\sqrt{3}}.\)

In fact for any \(y_{0}\in\mathbb{R}\) the IVP \[\frac{dy}{dx}=6y^{2}x,\quad\quad y(0)=y_{0},\] has the solution \[y(x)=\frac{1}{y_{0}-3x^{2}}\text{ on the interval }I=[0,\frac{y_{0}}{\sqrt{3}}),\] with the exception of \(y_{0}=0\): there is no solution in the family ([eq:ch3_fo_sep_first_example_ansatz]) which solves the IVP with \(y_{0}=0.\)

\(\text{ }\) Summary. Miraculously, the seemingly nonsense computations ([eq:ch3_fo_first_example_1])-([eq:ch3_fo_first_example_res_3]) led to a whole family of actual bona-fide solutions to the ODE ([eq:ch3_sep_first_example]). The crucial part of the nonsense computation was the separation that is expressed in ([eq:ch3_fo_first_example_1]): \(y\) only appears on the l.h.s. and \(x\) only appears on the r.h.s. Whenever an ODE can be written in a factored form \[\frac{dy}{dx}=\frac{p(x)}{q(y)}\tag{3.79}\] one can carry out an analogous heuristic computation after “splitting” \(\frac{dy}{dx}.\) One obtains \["q(y)dy=p(x)dx",\] and if both sides can be integrated one obtains an ansatz for a solution that can then be verified rigorously.

\(\text{ }\) Other examples. Let us try this procedure for linear first order ODEs.

Example 3.26 • Solving first order autonomous linear ODE using separability For \(a,b\in\mathbb{R}\) consider the ODE \[\frac{dy}{dx}=ay+b,\] which was the topic of Section 3.2. Note that we can write this in the separated form \["\frac{dy}{ay+b}=dx".\] Integrating both sides we arrive at \[\frac{1}{a}\log(ay+b)=x+c,\] for arbitrary \(c\in\mathbb{R}.\) Solving for \(y\) this gives \[y=e^{ca}e^{ax}-\frac{b}{a}.\] Letting \(\alpha=e^{ca}\) this recovers the family ([eq:ch3_prop_fo_lin_all_sols_sol_formn]), which we proved in Proposition 3.13 were indeed solutions (and in fact the only solutions).
Example 3.27 • Solving first order non-autonomous linear homogeneous ODE using separability For a function \(x\to a(x)\) consider the ODE \[\frac{dy}{dx}=a(x)y,\] which is the class of ODEs considered in Section 3.5 with \(b(x)=0.\) This has the separated form \["\frac{dy}{y}=a(x)dx"\] Integrating both sides we arrive at \[\ln y=\int_{t_{0}}^{x}a(s)ds+c\] for arbitrary \(t_{0},c\in\mathbb{R}.\) Solving for \(y\) this gives \[y=\exp\left(\int_{t_{0}}^{x}a(s)ds+c\right),\] which is equivalent to \[y=\alpha\exp\left(\int_{t_{0}}^{x}a(s)ds\right),\] for arbitrary \(\alpha.\) Again we have recovered the family of Section 3.25 when \(b(x)=0,\) which we proved in Proposition 3.24 were indeed solutions on any interval where \(a\) is continuous and integrable (and in fact the only solutions).

\(\text{ }\)Rigorous theorem. We will now prove that this trick does indeed produce solutions for any ODE in the class ([eq:ch3_fo_sep_first_genereal_separability]). Let us first formally define the class.

Definition 3.28 • Separable first order ODE

Any first order ODE of the form \[q(y)\frac{dy}{dx}=p(x),\quad\quad t\in I,\tag{3.81}\] for an interval \(I\) and functions \(p,q:I\to\mathbb{R}\) is called separable.

The trick above can be made less improper by noting that if \(Q(y)\) is a differentiable function such that \(Q'(y)=q(y),\) then the chain rule gives that \[\frac{d}{dx}Q(y(x))=Q'(y(x))\frac{dy}{dx}=q(y)\frac{dy}{dx}.\] (This needs no quotation marks, as it is a proper well-defined equality with indeed follows rigorously from the assumption on \(Q\)). Thus if such \(Q\) exists then ([eq:ch3_sep_formal_del]) implies that \[\frac{d}{dx}Q(y(x))=p(x).\] If also \(P(x)\) is such that \(P'(x)=p(x)\) we obtain by integrating both sides (again, these are properly well-defined integrals) to obtain from ([eq:ch3_sep_formal_del]) that \[Q(y(x))=P(x)+c,\] for some \(c\in\mathbb{R},\) for any solution \(y\) of ([eq:ch3_sep_formal_del]). If \(Q\) has an inverse \(Q^{-1}\) then \[y(x)=Q^{-1}(P(x)+c)\] for any solution \(y.\) Let us now dot all the \(i\)-s and cross all the \(t\)-s in the above argument to arrive at the following formal theorem.

Theorem 3.29

Let \(I,Y\subset\mathbb{R}\) be intervals and \(p:I\to\mathbb{R},q:Y\to\mathbb{R}\) be continuous functions. For any \(x_{0},x\in I\) define \(P(x)=\int_{x_{0}}^{x}p(s)ds,x\in I,\) and for any \(y_{0},y\in Y\) define \(Q(y)=\int_{y_{0}}^{y}q(y)dy.\)

Then \(y:I\to Y\) is a solution of the separable ODE \[q(y)\frac{dy}{dx}=p(x),\quad\quad x\in I,\tag{3.83}\] iff \(y\) is differentiable and \[Q(y(x))=P(x)+c,\quad\quad x\in I,\tag{3.84}\] for some \(c\in\mathbb{R}.\)

Proof. By the fundamental theorem of calculus the continuity of \(p,q\) implies that \(P,Q\) as defined are differentiable and \(P'(x)=p(x)\) and \(Q'(y)=q(y).\)

\(\impliedby\): Assume that \(y:I\to Y\) is a differentiable function such that ([eq:ch3_thm_sep_sol]) holds, i.e. such that \[Q(y(x))=P(x)+c,\quad\quad\forall x\in I.\] The r.h.s. is differentiable by assumption, and by the chain-rule and assumption the l.h.s. is too. It follows that \[Q'(y(x))\frac{dy}{dx}=P'(x),\quad\quad\forall x\in I,\] and again by assumption this implies ([eq:ch3_thm_sep_ODE]).

\(\implies:\) Assume that \(y\) is a solution of ([eq:ch3_thm_sep_ODE]) taking values in \(Y,\) i.e. a differentiable function \(y:I\to Y\) that satisfies ([eq:ch3_thm_sep_ODE]). By the chain rule \(x\to Q(y(x))\) is differentiable on \(I\) and \[\frac{d}{dx}Q(y(x))=Q'(y)\frac{dy}{dx}=q(y)\frac{dy}{dx}.\] Thus ([eq:ch3_thm_sep_ODE]) implies that \[\frac{d}{dx}Q(y(x))=p(x),\quad\quad x\in I.\] By the fundamental theorem of calculus applied on both sides this implies that for any \({x,x'\in I}\) \[Q(y(x))-Q(y(x'))=P(x)-P(x'),\] which implies that ([eq:ch3_thm_sep_sol]) holds with \(c=Q(y(x'))-P(x').\)

Remark 3.30

a) Some of the problems in exercise 3, 4, 5 on exercise sheet 2 can be solved with the methods of this section.
b) If you are solving a given concrete separable first order ODE, it is recommended that you use the non-rigorous separation trick ([eq:ch3_fo_first_example_1])-([eq:ch3_fo_first_example_res_3]) to derive an ansatz that you then check is indeed a solution, rather using the formula ([eq:ch3_thm_sep_sol]).

3.7 Failure of global existence

In this section we give an example of an ODE which fails to admit the existence of a global solution.

\(\text{ }\)Global existence guarantees in the first order linear case. We saw in Section 3.2 (Proposition 3.15) that every first order autonomous linear IVP with initial time \(t_{0}\) has a solution on the interval \([t_{0},\infty).\) These solutions are always truly global. We saw in Section 3.5 (Corollary 3.25) that an explicit first order linear IVP with initial time \(t_{0}\) has a solution any interval \([t_{0},t_{1})\) such that the coefficients \(a(t),b(t),\) are continuous and integrable on \([t_{0},t_{1}),\) including if \(t_{1}=\infty\) (and similarly for non-initial time constraints). Thus on an interval \(I\) on which \(a(t),b(t)\) are “well-behaved” there exists a solution globally on \(I\) - this is almost as good as for the non-autonomous case. For instance for the IVP \[\frac{dy}{dt}=\frac{1}{1+t^{2}}y,\quad\quad y(t_{0})=y_{0}\] (i.e. \(a(t)=\frac{1}{1+t^{2}}\) and \(b(t)=0\)) the function \[y(t)=y_{0}e^{\int_{t_{0}}^{t}\frac{1}{1+s^{2}}ds}\] is well-defined globally for all \(t\in[t_{0},\infty),\) and satisfies the ODE globally for these \(t,\) in addition to the initial constraint at \(t=t_{0}.\) Here we have the same very global solution as in the linear autonomous case. The worst-case for linear non-autonomous ODEs are those like \[\frac{dy}{dt}=\frac{1}{1-t^{2}}y,\quad\quad t\in(-'1,1),\tag{3.86}\] with \(a(t)=\frac{1}{1-t^{2}}\) which is not well-defined on all of \(\mathbb{R}\) but instead on a smaller interval - e.g. \(I=(-1,1)\) in this case. Nevertheless, for any \(t_{0}\in(-1,1)\) and \(y_{0}\in\mathbb{R}\) the function \[y(t)=y_{0}e^{\int_{t_{0}}^{t}\frac{1}{1-s^{2}}ds},\quad\quad t\in(-1,1),\] is well-defined at least on all of \((-1,1)\) and satisfies the ODE on this interval, in addition to initial condition.

\(\text{ }\)Counter-example showing failure of global existence. In this section we give an example showing that for more general first order IVPs we can not expect even the latter weaker form of global existence of solutions. The example is a separable equation, and this allows us to nevertheless explicitly solve the equation on the maximum possible interval with initial time \(t_{0}\) on which a solution exists.

Lemma 3.31 • IVP for which global existence fails

a) The IVP \[\frac{dy}{dt}=y^{2},\quad\quad t\in\mathbb{R},\quad\quad y(0)=y_{0}>0,\tag{3.88}\] has no solution.

b) The IVP \[\frac{dy}{dt}=y^{2},\quad\quad t\in I,\quad\quad y(0)=y_{0}>0,\tag{3.89}\] has a solution iff8 \(I=[0,t_{1})\subset[0,\frac{1}{y_{0}})\) and if so the unique solution is \[y(t)=\frac{1}{\frac{1}{y_{0}}-t},\quad\quad t\in[0,t_{1}).\tag{3.90}\]
Remark 3.32

a) The point here is that the relation \(\frac{dy}{dt}=y^{2}\) itself is well-defined for all \(t\in\mathbb{R}\) - unlike the example the first order linear example ([eq:ch3_fo_lin_a_not_defiend_everywhere]) - but nevertheless there is no solution valid for all \(t\in\mathbb{R}.\)

b) One sees from the form ([eq:ch3_non_glob_exist_uniq_sol]) that the issue is that the unique solution explodes as it approaches \(t=\frac{1}{y_{0}}\) - “blow-up in finite time”. Indeed \(y^{2}\) - the r.h.s. of this ODE - grows fast for \(y\) large. Compare to the IVP \[\frac{dy}{dt}=y,\quad\quad y(0)=y_{0}\] which has r.h.s. that also grows to infinity for \(y\to\infty,\) but slower than \(y^{2}.\) This is a first order linear ODE with constant coefficients and has the unique solution \[y(t)=y_{0}e^{t},\quad\quad t\ge0,\] which does grow \(\infty\) as \(t\to\infty,\) but remains finite for all finite \(t.\) To summarize, the r.h.s of the ODE ([eq:ch3_non_glob_exist_IVP_all_R]) grows too fast, so that finite time blow-up prevents global existence of solutions.

c) Later when we study the existence of solutions to a general explicit first order IVPs of the form \[\frac{dy}{dt}=H(t,y(t)),\quad\quad y(t_{0})=y_{0},\] we will only aim only to show existence locally for a small interval \(I=[t_{0},t_{0}+\varepsilon),\) for small enough \(\varepsilon>0.\) The counter-example ([eq:ch3_non_glob_exist_IVP_all_R]) shows that we cannot hope for global existence in general, even on a interval \(I\) on which \(t\to H(t,y)\) is well-defined.

Proof of Lemma 3.31. Part b) implies part a), so we only need to prove part b). Assume9 \(I=[0,t_{1})\) for some \(t_{1}>0.\) Any solution of ([eq:ch3_non_glob_exist_IVP_I]) satisfies \(\frac{dy}{dt}=y^{2}\ge0\) for all \(t\in I.\) Thus for \(t\ge0\) it holds that \(y(t)\ge y_{0}>0.\) Therefore any solution of ([eq:ch3_non_glob_exist_IVP_I]) is also a solution of the ODE \[\frac{1}{y^{2}}\frac{dy}{dt}=1,\quad\quad t\in I,\] which is of the form ([eq:ch3_thm_sep_ODE]) with \(Y=(0,\infty)\) and \(q:(0,\infty)\to\mathbb{R}\) given by \(q(y)=\frac{1}{y^{2}}\) and \(p(t)=1.\) Thus with \(Q:(0,\infty)\to\mathbb{R}\) given by \(Q(y)=-\frac{1}{y}\) so that \(Q'(y)=\frac{1}{y^{2}}=q(y),\) and \(P(t)=t\) so that \(P'(t)=1=p(t),\) it follows from Theorem 3.29 that every solution of ([eq:ch3_non_glob_exist_IVP_I]) satisfies \[Q(y(t))=P(t)+c,\quad\quad\forall t\in I,\] for some \(c\in\mathbb{R}.\) More explicitly \[-\frac{1}{y(t)}=t+c,\quad\quad\forall t\in I.\] A solution which also satisfies the initial condition \(y(0)=y_{0}\) then in fact satisfies \[-\frac{1}{y(t)}=t-\frac{1}{y_{0}},\quad\quad\forall t\in I.\tag{3.91}\] If \(t=\frac{1}{y_{0}}\) then this implies that \(-\frac{1}{y(t)}=0\) which is a contradiction. Thus we must have that10 \(I=[0,t_{1})\) for \(t_{1}<\frac{1}{y_{0}}\) if ([eq:ch3_non_glob_exist_IVP_I]) is a solution.

If so, then for \(t\in I\) the statement ([eq:ch3_non_gloabl_exist_thm_implicit_uniq_sol]) implies that \[y(t)=\frac{1}{\frac{1}{y_{0}}-t},\quad\quad\forall t\in I.\]

In exercises 5, 6 of exercise sheet 2 the content of this section is relevant.

3.8 Failure of local uniqueness

In this section we give an example of a first order explicit IVP that has several distinct solutions, i.e. uniqueness fails.

This is in contrast to the first order linear ODEs of Section 3.2 and Section 3.5 for which all IVPs had unique solutions (Proposition 3.15 and Corollary 3.25). It’s also in contrast to the IVP ([eq:ch3_non_glob_exist_IVP_I]) of the previous section that failed to admit a globally defined solution, but on the maximal interval on which a solution could be defined that solution was unique.
Lemma 3.33 • IVP for which local uniqueness fails

Let \(\varepsilon>0.\) Consider the explicit first order autonomous IVP \[\frac{dy}{dt}=|y|^{1/2},\quad\quad t\in[0,\varepsilon),\quad\quad y(0)=0.\tag{3.93}\] For any \(s\ge0\) define \[y:[0,\varepsilon)\to[0,\infty),\quad\quad y(t)=\begin{cases} 0 & \text{ if }t\le s,\\ \frac{1}{4}(t-s)^{2} & \text{for }t>s. \end{cases}\tag{3.94}\] Then \(y\) is differentiable and a solution of ([eq:ch3_example_local_uniq_fail_IVP])

Remark 3.34

The IVP ([eq:ch3_example_local_uniq_fail_IVP]) thus has an infinite family of distinct solution for any \(\varepsilon>0.\) One aspect of this IVP that is not “well-behaved” is that \(\frac{d}{dy}|y|^{1/2}\) is not well-defined for \(y=0\) (for \(y>0\) it holds \(\frac{d}{dy}|y|^{1/2}=\frac{1}{2}\frac{1}{|y|^{1/2}}\) which explodes as \(y\downarrow0\)). The general existence and uniqueness theorem we later prove will s include the condition that the derivative in \(y\) of the r.h.s. is well-defined and continuous, which will preclude the behavior here and allow for the existence and uniqueness of solutions to an IVP locally, on \([t_{0},t_{0}+\varepsilon)\) for some small enough \(\varepsilon>0.\)

Proof of Lemma 3.33. First of all, note that \(y\) as defined in ([eq:ch3_example_local_uniq_fail_IVP_fam_of_osls]) is continuous: this is obvious on \([0,s)\) and \((s,\varepsilon)\) from the formulas for these two cases - a fortiori, \(y\) is also obviously differentiable on these intervals. Furthermore if \(t<s\) then \[\frac{dy}{dt}=0=\left|0\right|^{1/2}=|y|^{1/2},\] so the ODE is satisfied on \([0,s)\cap[0,\varepsilon).\) On the other hand if \(t>s\) then \[\frac{dy}{dt}=\frac{2}{4}(t-s)^{2-1}=\left|\frac{1}{4}(t-s)^{2}\right|^{1/2}=|y|^{1/2},\] so the ODE is also satisfied on \((s,\varepsilon).\) It thus remains to consider \(t=s.\)

Since \[\lim_{t\downarrow s}y(t)=\lim_{t\downarrow s}(t-s)^{\alpha}=0=\lim_{t\uparrow s}y(t),\] the function \(y\) is continuous also at \(t=s,\) so on all of \([0,\varepsilon).\) Furthermore \(y\) is differentiable not only on \([0,s)\) but also on \([0,s],\) with \(y'(t)=0.\) On \([s,\infty)\) the function \(y\) is also differentiable with \[\frac{dy}{dt}=\frac{2}{4}(t-s)^{2-1}=\frac{t-s}{2}.\] Thus \(y(t)\) is differentiable on \([0,\varepsilon)\setminus\{s\},\) and at \(t=s\) it has a well-defined left and right derivatives \(\frac{dy}{dt}(s^{-})\) and \(\frac{dy}{dt}(s^{+}),\) namely \[\frac{dy}{dt}|_{t=s^{-}}=0\quad\quad\text{ and }\quad\quad\frac{dy}{dt}|_{t=s^{+}}=\frac{s-s}{2}=0.\] Since the left and right derivatives agree even at \(t=s\) the function \(y\) is differentiable on all of \([0,\varepsilon),\) and \(\frac{dy}{dt}|_{t=s}=0=\left|0\right|^{1/2}=\left|y(s)\right|^{1/2}\) so that the ODE is satisfied also at \(t=s.\)

In exercises 5, 6 of exercise sheet 2 the content of this section is relevant.

Theory and Numerics of ODEs

Home

Contents

Weeks

✕